摘 要
机载激光雷达测深系统(ALB)凭借成本低、效率高、作业机动灵活,可同时获取水下、水上点云数据的优势而被广泛应用于海岸、岛礁地形测量以及水上水下一体化测绘任务。与ALS相比,ALB通常点云数据密度低、质量差、场景内目标物相对单一且存在无控/少控的局限,直接将ALS条带镶嵌模型应用于ALB数据效果往往不理想。针对ALB数据特点,本文提出一种由粗到精的条带拼接模型。改进Alpha Shapes算法实现条带重叠区域的快速准确识别;基于水-陆区域对应的点云数据精度、密度和空间特征不同的特点,本文根据海拔高度信息将点云分为水下和非水下(陆地)两部分进行区别处理;针对陆地点云数据建立了一种以法向量和曲率为特征的随机样本一致性(RANSAC)-ICP配准模型;针对水下点云数据设计了一种基于权重分配的由粗到精的拼接模型。分别采用3L算法优化的隐式b样条曲面拟合算法和最小二乘趋势面拟合算法对重叠条带进行权值分配,实现ICP粗配准和非刚性ICP精配准,并且在精配准模型中将空间拓扑约束项添加到非刚性ICP代价函数中,以防止异常值引起的过度变形。最后在与ICP方法的对比实验中,新模型条带拼接结果均方根误差(RMSE)为0.12 m,最大误差为0.36m,充分证明了其在精度和灵活性方面的优越性。
研究背景
目前,常规区域性水深测量方法主要是以舰船等水面移动载体为平台的声学探测技术,比如单波束测深系统和多波束测深系统。然而在水深小于10m的潮间带地区由于受到海洋潮汐的影响,往往存在滩浅、泥淤、礁石等较为复杂的作业环境,多数情况下只能依靠人工或小船乘潮作业的方式进行水深数据的采集,效率低、难度大,有一定危险性,故近海岸区域内长期以来存在大量测深数据空白。近年来,以航空平台为载体的激光测深技术有效地克服了传统测深方式周期长、机动性差、测深精度低、测区范围有限等缺点,受到了广泛关注。机载激光雷达测深系统是集激光系统、全球定位系统和惯性导航系统等于一体的主动遥感测深系统,简称ALB(Airborne LIDAR Bathymetry)。单波段ALB系统采用穿透水体能力较强的532nm蓝绿激光波段,如CATS系统、EAARL系统和Aquarius系统,双波段ALB系统通常会同时搭载1064 nm的红外激光系统进行陆地高程和水面高的测量,如Hawk Eye和CZMIL。ALB系统不仅能满足海岸带区域的水深探测需求,还能同时测量水上、水下三维地形,而无需进行数据融合,真正实现了水陆一体化无缝测量。
无论是多波束测深法还是机载lidar测深法都采用的是条带测深技术,条带测深已经成为全覆盖海洋测深的主要方式。如何探测和消除条带测深数据中的系统误差一直是海道测量界的研究难点。在全覆盖测量过程中,条带拼接是保证海底地形精度的重要环节。相邻条带之间的重叠区域内深度不符值往往用来检核和判定条带拼接质量。机载LiDAR测深经过系统多传感器标定校准、折射改正等处理后,其残余误差主要由校正残差构成。目前测深条带拼接方法有很多,但绝大多数只顾及水深偏差而忽略测深点空间结构信息。目前,针对ALS 3-D点云的条带拼接方法很多,常见的有ICP,CDP,NDT等,而针对机载lidar测深数据特点的条带拼接研究较少。由于水-陆点云数据精度、密度和空间结构特征偏差较大,传统的ALS条带拼接模型在寻找全局最优的过程往往会损失陆地点云的精度得不到理想的结果。
模型介绍
为了更好地消除校正残余误差,得到高精度的DEMs等数字产品本文在充分考虑ALB数据特点的前提下提出了一种由粗到精的条带拼接模型,如图1所示。

图1. 提出的条带拼接模型工作流程图
拼接模型大致可以概括为以下四步:
(1)预处理,经过定位定姿后的水深数据通常会有很多噪声值,在进行条带拼接时,为了避免这些噪声的干扰,需要进行滤波处理,本文采用局部拉普拉斯滤波算法进行滤波,对应图中的第一步操作。
(2)重叠区确定,由于ALB数据精度相对较低,地形平坦,特征信息不明显,尽管重叠条带点云是部分重叠的,没有绝对的包含关系,因此直接对条带数据进行匹配效果很差,需要对重叠区独立进行研究。为了减少计算量、提高计算速率,本文首先采用uniform降采样方法对点云数据进行抽稀,然后采用优化后的Alpha Shapes 算法提取条带边界线,最后利用PolyhedronIntersection算法提取重叠区点云数据。因为水上水下点云对应不同的条带拼接模型,需要利用海拔高度将点云分为水上部分和水下部分。对应图中的第二、三步操作。
(3)水下区域条带拼接,拼接模型的核心思想是将权重分布与配准算法相结合,前者的目的是为配准模型提供控制参考,对应图1中的第四步操作。粗配准过程中驱动3L算法进行IBS曲面拟合,根据检查条带和重叠条带的偏差为下一步ICP粗配准提供权值分配,理论上偏差越大,重量越小。精配准过程中对两个交叠的条带进行最小二乘趋势面拟合算法,通过计算从法线方向到不同条带的距离,为每个点赋予一个权值,进而为非刚性ICP精配准提供权重分配,同样,偏差越大,权重越小。为了削弱异常数据对条带拼接的干扰,文中在传统的非刚性ICP损失函数中增加空间结构拓扑约束项(Topological constraint term)包括迭代三角面片的差异之和以及三角面片坡度偏差之和。利用仿射变换阵对模板进行形变直到达到最大迭代次数或满足最小迭代偏差阈值则迭代停止。
(4)陆地区域条带拼接,对应图1中的第五步,其实现步骤可以分为四步:1)特征筛选,首先利用法向量变化程度和曲率特征进行特征点筛选,去掉点云中较为平坦的部分;2)初始特征点对确定,为每个特征点建立一个16维的特征向量,通过欧氏距离剔除大于阈值的匹配点对。分别对每个点对计算符合距离约束的点对数目,对正确配准点对数目进行排序保留优势初始匹配特征点对;3)RANSAC特征点筛选,使用RANSAC算法对优势特征点对进行检验,直到循环次数达到阈值得到刚体变换矩阵并进行粗配准;4)ICP精配准,为了进一步得到高精度配准结果,对重叠区域利用ICP算法进行精确配准。
结果分析
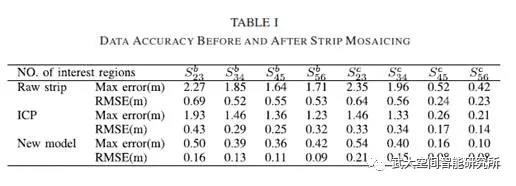
对实测的机载雷达测深数据进行条带拼接处理结果如下,在area B和area C中条带重叠区共选取了8个半径为10m的圆形区域,以最小二乘拟合面为真值计算计算最大误差和MRES,统计结果如表所示。8个感兴趣区域的RMSE为0.12 m,最大误差为0.36 m,优于ICP模型的RMSE为0.28 m和最大误差1.1 m。
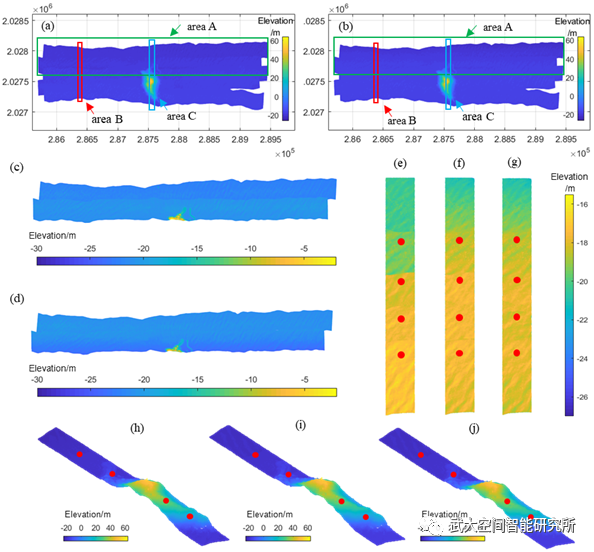
图3 条带拼接模型处理前后效果。(a)是原始测深条带,(b)是条带拼接模型处理后结果。(c)和(d)分别为area A条带拼接前后地形,(e),(f),(g)分别对应area C内原始数据,ICP模型和文中模型处理后地形,(h),(i),(j)分别对应area C内原始数据,ICP模型和文中模型处理后地形。
Abstract:Theairborne light detection and ranging (LiDAR) bathymetry (ALB) system is anextension of the ubiquitous topographic LiDAR mapping system and has been mostsimply characterized as adding a green laser to the infrared laser of toposystems. Due to the low point cloud density and monotonous objects in thescene, it is difficult to mosaicing the ALB strips. Therefore, the existingairborne laser scanning strip stitching algorithm has poor performance for ALBstrips. In this article, a coarse-to-fine strip mosaicing model for ALB isproposed. The framework is fast and efficient and can handle large ALB data. Animproved alpha shapes algorithm can fast and accurately determine the overlapregion of strip is applied. Due to different data accuracy and spatialcharacteristics, the water area and land area are processed separately. Aweight distribution-based coarse to fine registration model is designed forunderwater areas. The topological constraint term is added to the nonrigiditerative closest point (ICP) cost function to prevent excessive deformationcaused by outliers. The implicit B-spline surface fitting algorithm using the3L algorithm and the least-squares trend surface fitting algorithm are appliedseparately to assign weights for overlapping strips to solve the limitation ofno control or less control. Moreover, a random sample consensus (RANSAC)-ICPregistration model characterized by the normal vector and curvature is constructedfor land area. Finally, the comparisons with ICP highlight the superiority ofthe proposed approach in flexibility and accuracy. The root-mean-square error(RMSE) is 0.12 m and the maximum error is 0.36 m.